This semester we (Berit Johnson and Sarah Strohkorb) set out to answer some predictive questions about Olin courses, students, and majors. More specifically, we’re attempting to answer the question, “can we predict what one student will take for any given semester based on their course history?” which easily expands to, “can we predict Olin’s total course enrollment for Spring 2014 based on all of the students’ course histories?”
Our preliminary results show promise, but there is significant room for improvement. We’d like to share our work with the Olin community and also welcome feedback and suggestions.
Methods
To begin, our work depends on the assumption that Olin students act somewhat predictably: the courses people have taken in the past can tell us something about what they are likely to take in the future. We therefore obtained the anonymized list of all courses taken by each Olin student from the Fall 2002 semester to the Spring 2014 semester. This data became the input to our model.
To make our predictions, we used a logistic regression which is a model designed for classification and used to predict a binary outcome based on a set of predictors . We train the model by giving the model input data with known classifications. In this case, the input is the set of classes a student has taken up to a given point in their academic career and the classification is whether or not that student takes a given course in a particular semester. Once we have trained the model, we can verify its validity by using it to classify testing data that the model has never seen before.
In order to predict Olin’s entire course enrollment, we predicted the enrollment for each course individually, and within each course predicted the enrollment for each graduating class (first years, sophomores, etc.). For example, let’s say we’re predicting the enrollment of sophomores in Software Systems for the Spring 2014 semester. We extracted all of the current sophomores from the data set to form our “testing data.” We then created our training data by taking all of the other students’ course histories up to the first semester of their sophomore year and recording whether or not they took Software Systems during the second semester of their sophomore year.
We fit our logistic regression model to the training data and used the model to make predictions based off of the testing data. In this example, for every current sophomore the model outputs a probability that they will take Software Systems. Summing these probabilities yields the expected number of sophomores to enroll in Software Systems in Spring 2014.
Results
We compared our predicted enrollment for each course this semester with the actual enrollment and displayed representative results for seven of the courses offered in the Spring 2014 semester in Figure 1. Of the 57 courses we predicted enrollment for, 9 had less than 10% error, 7 had 10-30% error, 12 had 30-50% error, and 29 had over 50% error. We also compared our model to the enrollment for the previous year as a baseline. We can see that when our model does well, it does very well, out-performing the baseline, but when it does poorly, it does very poorly indeed.
Our analysis of the predictions suggests that our model performs poorly for newer courses like Data Science and other “Special Topics” courses because there is no history of students taking these courses. The courses that our model does well with tend to be more well-established like Thermodynamics or PDE’s. Additionally, for courses like POE, Signals & Systems, and Software Design, enrollment can vary due to variance of student interest, trends within graduating classes, and how the course is advertised. There are also a variety of factors that can affect enrollment that our model does not take into account such as enrollment caps or whether a given course satisfies a major requirement.
Future Work
One problem that we encountered with our data was the amount of variance in the Olin curriculum from special topics that are only offered once to changes in the First year curriculum. In order to improve the quality of our predictions, we could group related classes and predict whether or not students are likely to take a course in a particular group.
Additionally, we are considering answering other questions with this data such as: “who is likely to wait until senior year to take Mod Bio?”, “what major is person X most likely going to graduate with?”
If you have any feedback/suggestions or questions you think would be interesting to try to answer with this data, please let us know!
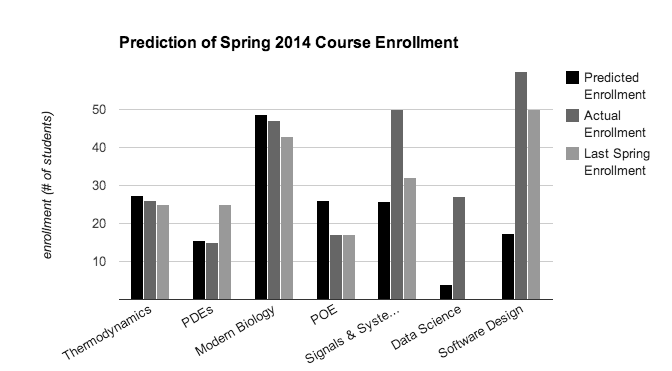Figure 1. A comparison of predicted, actual, and last Spring’s course enrollment for a particular set of courses for the Spring 2014 semester. The predicted enrollments were determined by the output of our logistic regression model. PDEs stands for Partial Differential Equations and POE stands for Principles of Engineering.
